Často se uvádí, že numerické metody jsou současně vědou i uměním. Využívá se zde postupů, kdy při procesu řešení matematické úlohy zformulované na základě znalosti problému lze dojít k řešení úlohy s využitím pouze aritmetických a logických operací. V praxi to znamená, že pomocí numerických metod lze vyřešit problémy, které nejdou řešit přímo, nebo by řešení bylo příliš složité, časově a ekonomicky náročné. Výsledky řešení jsou přibližné. Nepřesnost (tzv. chyba), která vzniká při numerickém řešení, je udávána pouze jako odhad chyby (mnohdy pesimistický), neboť přesné řešení není známo. Máme na mysli tzv. chybu metody. Chyby vzniklé při formulaci matematického problému zanedbáním některých skutečností (použitím modelu), tvoří další skupinu chyb, se kterými je nutno někdy počítat. Tyto nepřesnosti jsou však často zanedbávány. Při výpočtech předpokládáme v současnosti výhradně použití počítačů. Často je k dispozici několik možných postupů výpočtu; to dává s ohledem na typ funkce možnost výběru vhodné metody. Každá metoda má výhody, ale i nevýhody. Dále jsou jednotlivé postupy stručně popsány. Implementaci metod je věnován závěr tohoto dokumentu.

Řešení nelineárních rovnic

Tato část je věnována řešení nelineárních, algebraických i transcendentních, rovnic jedné reálné proměnné. Omezíme se na případ určování reálných kořenů těchto rovnic.

Problematiku lze rozdělit na dvě základní části:

1. Hledání reálných kořenů rovnice f(x) = 0 na intervalu <a, b>, kde x je reálná proměnná a f(x) je funkce této proměnné. Např.: ; kořen

2. Hledání reálných kořenů rovnice P(x) = 0, kde P(x) je polynom a_nxⁿ + a_n-1x^n-1 + … a₁x + a₀např.: ;

Hledáme reálné číslo α pro které platí f(α) = 0; α je kořen rovnice f(x) = 0. Hledání komplexních kořenů obecné rovnice f(x)= 0 se vyskytuje poměrně zřídka. Numericky (jak známo) řešíme úlohy v případě, kdy nelze nalézt řešení v uzavřeném tvaru, ale lze vymyslet efektivní algoritmus (dnes prakticky vždy implementovaný na počítači), pro řešení této úlohy. V případě nelineární rovnice, o který se zde zajímáme, musíme hledat metody, které vedou k přibližnému řešení. Při určování kořene rovnice je u některých metod požadováno, aby byl separován kořen rovnice (tj. aby byl určen interval, ve kterém leží jediný kořen). Separaci lze provést několika způsoby. Můžeme např. vyšetřit průběh funkce a z funkce f(x) spočítat první a druhou derivaci. Z průběhů derivací lze zjistit, ve kterých intervalech je funkce rostoucí a klesající a vyšetřit pak lokální minima a maxima. Je důležité si uvědomit, že reálné kořeny rovnice jsou průsečíky grafu funkce a osy x. Zjištěné intervaly potom použijeme pro přibližný výpočet kořenů. Na počítači provádíme většinou separaci interakčně na základě znalosti grafického průběhu funkce f(x) nebo P(x) („grafická“ separace kořenů rovnice) neboť zjišťování průběhů derivací je mnohdy obtížné.

V této části uvedeme některé postupy vedoucí k řešení nelineárních rovnic „iteračním“ způsobem (iteratio = opakování). Při volbě metody je nutno zodpovědět dvě základní otázky:

1. Konvergují dané iterace k hledanému kořenu?

2. Pokud ano, jaká je rychlost konvergence?

Druhá otázka však dnes do značné míry ztrácí na důležitosti, neboť při implementaci metod na počítači je rychlost výpočtu vyhovující. Pokud se týká konvergence:

a) buď záleží na počáteční aproximaci kořene rovnice f(x) =0 nebo

b) iterační metoda konverguje nezávisle na volbě počáteční aproximace

V každém případě je nutno vždy prozkoumat průběh funkce. Otázka jak blízká má být tato aproximace k hledanému kořenu souvisí s úlohou ukončení výpočtu. V praktických případech máme obvykle dostatek apriorních informací o uvažovaném kořenu (známe např. graf funkce), takže konvergence iteračních metod nebývá problémem. Je-li apriorní informace chudá, musíme užít metodu, jejíž konvergence nezávisí na volbě počáteční aproximace (např. metodu bisekce); ta ale konverguje „pomalu. Po získání „dobré“ aproximace lze v případě potřeby přejít k rychleji konvergující metodě. Srovnávat vlastnosti konvergence metod, jejíž konvergence závisí na počáteční aproximaci, je teoreticky nesnadné, ale v současnosti nemusí být směrodatné.

Je však možné a důležité (zejména v oblasti speciálních aplikačních oblastí jako je regulace a automatizace výrobních procesů, kosmické projekty atd.) srovnávat relativní rychlosti konvergence různých iteračních metod. Efektivnost dané metody závisí tedy na počtu vyčíslování funkce f(x) a případně i jejích derivací. Ve speciálním případě algebraické rovnice není obvykle k disposici dobrá apriorní informace o kořenu a kromě toho u rovnice P(x) = 0 je někdy třeba určit všechny kořeny, kdežto u rovnice f(x) = 0 se obvykle zajímáme pouze o jeden kořen. V tomto dokumentu však pro řešení rovnic P(x) = 0 užíváme tytéž metody jako pro řešení rovnic f(x) = 0. Obecně klademe na metody, jejichž konvergence je zaručena nezávisle na počáteční aproximaci, větší důraz. Z tohoto pohledu většině uživatelů postačí dále probíraná metoda půlení intervalu (metoda bisekce).

Konverguje-li nějaká iterační metoda pro řešení rovnice f(x) = 0, potom jediné omezení přesnosti, se kterou je kořen vypočítán, je v počtu cifer, s nimiž se provádí výpočet. To znamená, že důležité omezení přesnosti spočívá mnohdy (a to je podstatou problému) v zaokrouhlovací chybě v jedné iteraci. Metody řešení nelineárních rovnic lze rozdělit podle konvergence na:

metody vždy konvergentní
metody, které nemusí vždy konvergovat

Jiný způsob rozdělení na metody:

Stacionární (ve všech krocích výpočtu používá se jeden rekurentní vztah)
Nestacionární (při výpočtu se v daném kroku rozhodujeme mezi dvěma možnými vztahy)

Způsob ukončení výpočtu: většinou se užívá metoda testování, zda je výsledná hodnota v intervalu požadované nepřesnosti nebo se výpočet ukončuje po vykonání určitého počtu kroků.

Přesnost řešení závisí na mnoha okolnostech. Na použité metodě, počítači, programu (který je implementací určitého algoritmu) vstupních hodnotách (jejich věrohodnosti) atd.

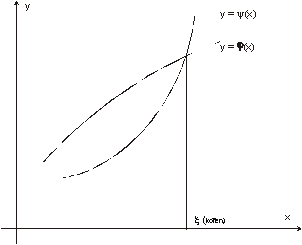
Grafické metody řešení nelineárních rovnic

U rovnice

udávají průsečíky grafického znázornění funkce f(x) s osou x polohu kořenů. Většinou je chápeme jako hrubé aproximace kořenů (kořene) - počáteční (startovací) hodnoty v algoritmech metod.

Mnohdy lze vyjádřit předchozí rovnici ve tvaru:

tj.

x-ové souřadnice průsečíků grafů a jsou pak hledané kořeny.

Metoda půlení intervalu (bisekce)

Jedná se o vždy konvergentní, nestacionární a dá se říci univerzální metodu, která se dá použít ve většině praktických případů.

Aby bylo možno metodu užít, musí být splněny dvě podmínky. První je požadavek, aby funkce f byla spojitá pro "x Î I₀ = <a₀, b₀>. Druhou podmínkou je, aby funkční hodnoty v krajních bodech zvoleného intervalu měly opačná znaménka tj. musí platit f(a₀) f(b₀) < 0. Pokud jsou obě podmínky splněny, pak tato metoda vždy konverguje. Princip metody půlení intervalu je znázorněn na následujícím obrázku.

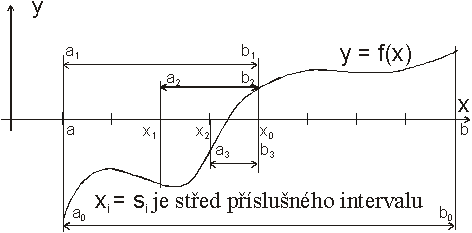
Polohu kořene zjišťujeme rozpůlením intervalu <a_i, b_i> a zjištěním, ve které části kořen leží. Zmenšený interval, v němž leží kořen lze dále rozpůlit a tak zvyšovat přesnost výpočtu. Střed posledního sestrojeného intervalu lze považovat za aproximaci kořene řešené rovnice. Z tohoto postupu je patrné, že čím více kroků provedeme, tím přesnější dostaneme výsledek.

Algoritmus metody ve Visual Basicu:

e = Přesnost

a0 = DolníMez

b0 = HorníMez

s1 = (a0 + b0) / 2

If y(s1) = 0 Then

MsgBox "Přesná hodnota kořene je: " & s1

Exit Do

End If

If y(a0) * y(s1) < 0 Then

b0 = s1

Else

a0 = s1

End If

Loop Until Abs(b0 - a0) < e

MsgBox "Přibližná hodnota kořene je: " & s1

Pokud potřebujeme zjistit odhad pro maximální možnou odchylku kořene u této metody, pak můžeme použít pro odhad chyby následující vzorec:

kde n je počet kroků a a₀dolní mez intervalu a b₀ je horní mez intervalu. Z tohoto vzorce se dá určit z požadovaného počtu platných míst - tedy z požadované přesnosti určení kořene požadovaný počet kroků a tedy i doba výpočtu; počet kroků:

Metoda tětiv (regula falsi)

Tětiva je úsečka (část přímky) spojující dva body křivky. Křivka se nahradí v daném intervalu přímkou. Průsečík této přímky s osou x je zpřesnění kořene. Metoda regula falsi je konvergentní pro všechny spojité funkce. Obecně se jedná o nestacionární metodu, mnohdy (např. u konvexních funkcí, kdy je druhá derivace kladná) je stacionární - jeden krajní bod intervalu je vždy jedním ze dvou bodů užitých v následující iteraci. Tato metoda je velmi vhodná v případě, že nejsou známy výchozí údaje o poloze kořenu; konverguje však relativně pomalu. Stačí ale nalézt pouze dva body, ve kterých má hodnota funkce opačné znaménko a pak tuto metodu lze aplikovat na zadaný interval. Princip metody je znázorněn na následujícím obrázku.

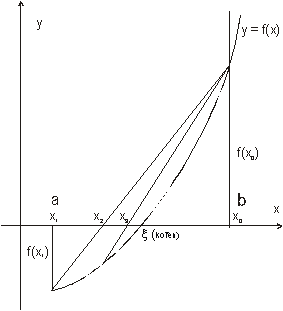
Pro výpočet následující aproximace kořenu x_i+1 použijeme vztah

Tento vzorec platí pouze pro funkce, pro které je metoda regula falsi stacionární (tj. nemění-li funkce v intervalu svůj charakter) pravým krajním bodem intervalu na obrázku je po celou dobu výpočtu bod x₀; obecně je to však nestacionární iterační metoda. Obecný vztah je:

kde x_a a x_b jsou předchozí vypočtené aproximace kořenu s rozdílným znaménkem hodnoty funkce f(x).

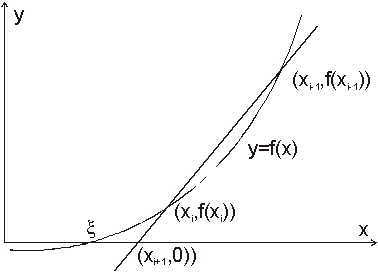
Metoda tečen (Newtonova metoda)

Newtonova metoda tečen využívá k nalezení kořenu rovnice tečny. Křivku v okolí kořene nahrazujeme tečnou v bodě Průsečík tečny s osou x (jeho x-ová souřadnice) je nová aproximace kořene . Vycházíme z toho, že z hodnoty první derivace funkce v určitém bodě se dá určit rovnice tečny procházející tímto bodem. Pokud metoda konverguje, konverguje většinou rychleji než metoda bisekce.

Pro výpočet pomocí Newtonovy metody tečen se užívá jednoduchý vztah

kde x_i je aproximace (pro i=0, tj. na začátku výpočtu je to zvolená hodnota) kořene rovnice a x_i+1 je následující, upřesněná aproximace.

Pokud lze pro daný problém použít Newtonovu metodu (je však např. nutno znát vztah pro první derivaci funkce), pak je to velmi vhodné, neboť algoritmus metody je jednoduchý.

Lze očekávat při každé iteraci dojde ke zdvojnásobení počtu platných číslic. Pro odhad chyby lze použít vzorec

m je minimum hodnoty první derivace v intervalu od počáteční aproximace ke kořeni. Nevýhodou této metody je ovšem to, že nemusí konvergovat vždy. Také kriterium použitelnosti může značně omezit oblast jejího používání:

funkce musí být v okolí kořene spojitá

funkce nesmí mít v okolí kořene nulovou derivaci a musí být splněna podmínka

Dále se použití této metody liší podle toho, zda je funkce v daném intervalu konvexní, nebo konkávní. Typ funkce lze zjistit v daném bodě pomocí hodnoty funkce a hodnoty druhé derivace. Pro konvexní funkci platí podmínka podle vztahu

f(x)>0 AND f’’(x} >0

Pro konkávní funkci platí podmínka

f(x)<0 AND f’’(x} <0

Řešení je pro konvexní i konkávní funkce stejné, pouze je zapotřebí jinak volit výchozí bod. U konvexních funkcí je zapotřebí zvolit výchozí bod nad očekávaným kořen a přibližovat se k němu shora. U konkávních funkcí je třeba zvolit výchozí pod kořenem a ke kořenu se přibližovat zdola. Princip Newtonovy metody pro konvexní funkce je znázorněn na následujícím obrázku

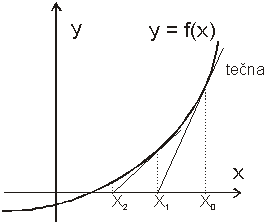
Metoda sečen (sekantová metoda)

Sečna (sekanta) je přímka protínající křivku. Vztah pro metodu sečen lze jednoduše odvodit např. ze vztahu metody tečen. Metoda se užívá zejména v případech, kdy derivace je dána příliš složitým vztahem. Nezaměňujte ji však s metodou tětiv! Nekonverguje vždy, je ale stacionární. Oproti metodě regula falsi se (v případě konvergence) jedná o podstatné zlepšení výpočtu. Lze použít následující rekurentní předpis:

Viz následující obrázek:

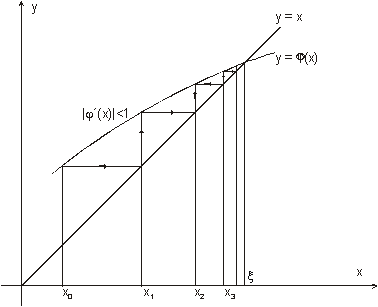
Přímá iterační metoda

Rovnice f(x)=0 se nahradí rovnocennou rovnicí ve tvaru x=j(x). Funkci j nazýváme iterační funkcí. Dále se zvolí počáteční aproximace kořene x₀rovnice a další aproximace se počítají podle jednoduchého vztahu

x_k+1= j(x_k) k = 0,1,2,…dokud | x_k+1 - x_k | ³ d, kde d > 0 je zvolené číslo

Konvergence metody a pracnost výpočtů závisejí na vhodné volbě iterační funkce a na počáteční aproximaci. Podmínky konvergence této metody jsou:

V daném intervalu musí být funkce spojitá a . Princip iterační metody je ukázán na obrázku:

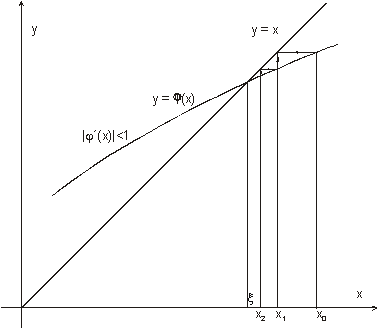
Nebo:

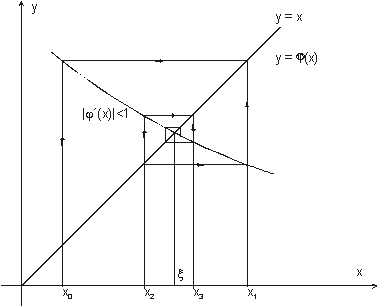
Z obrázků vyplývá, že z hlediska minimalizace chyby je vhodná taková iterační funkce, jejíž derivace je v okolí kořene blízká nule. Pokud je derivace v okolí kořene jen o málo menší než jedna, pak je vhodné zvolit jinou iterační funkci, nebo použít jinou numerickou metodu. Jestliže je derivace v okolí kořene větší než jedna, pak je nutné nahradit funkci j inverzní funkcí y.

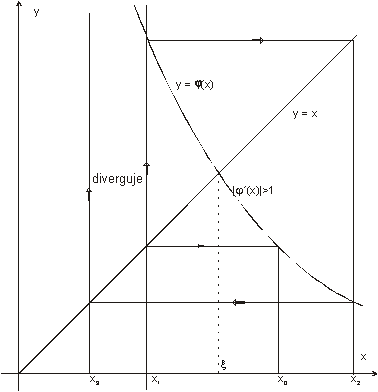
Při použití iterační metody se nemusíme obávat chyb vzniklých zaokrouhlováním.

Aproximace funkcí

Aproximace

Aproximace je náhrada (složité) funkce nebo vyjádření funkce zadané pouze tabulkou funkcí jednodušší (například polynomem). Tabulkové hodnoty představují buď přesné hodnoty funkce nebo hodnoty zatížené chybami (získané např. měřením).

Aproximace interpolací

Pokud se funkční hodnoty f(x_i) funkce, zadané tabulkou:

x_i	x₀	x₁	x₂	…	x_n-1	x_n
y_i = f(x_i)	y₀	y₁	y₂	…	y_n-1	y_n

shodují v n+1 bodech (uzlech interpolace) s hodnotou polynomu P(x_i), tj. f(x_i) = P(x_i), i=0, 1, …, n, jedná se o interpolační aproximaci nebo stručně interpolaci (a sice interpolaci polynomem n-tého stupně)

P_n (x) = a_nxⁿ + a_n-1x^n-1 + … a₁x + a₂x² + a₀

Hledáme takový polynom, aby platilo: P_n (x₀) = f(x₀), P_n (x₁) = f(x₁), …, P_n (x_n) = f(x_n), tedy v daných bodech souhlasí hodnoty aproximační funkce s hodnotami aproximované funkce.

Získáme soustavu n+1 rovni o n+1 neznámých (koeficienty a_i); x_i a f(x_i) jsou známé hodnoty. Soustavu lze jednoduše řešit, např. v aplikaci Excel, pomocí inverzní matice.

Jiný způsob určení koeficientů interpolačního mnohočlenu je užití Lagrangeova tvaru interpolačního mnohočlenu:

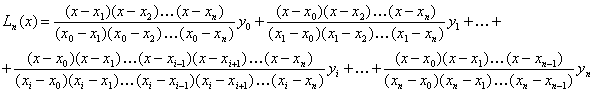
Aproximace metodou nejmenších čtverců pomocí polynomů

Metoda nejmenších čtverců patří mezi metody aproximace funkce, při níž je f(x_i) funkce a {x_i}, i=1,…, n posloupnost bodů neboli argumentů, v nichž jsme naměřili hodnoty funkce f(x), které jsou obecně zatíženy chybami a koeficienty se volí z podmínky, aby součet čtverců rozdílů mezi funkcí f(x) a její aproximací na konečné množině bodů byl minimální. Předpokládáme, že chyby v různých bodech jsou na sobě navzájem nezávislé. Funkci je tedy zadána tabulkou:

x_i	x₀	x₁	x₂	…	x_n-1	x_n
y_i = f(x_i)	y₀	y₁	y₂	…	y_n-1	y_n

Hledáme mnohočlen m-tého stupně (kde m < n):

P_m (x) = a_mx^m + a_m-1x^m-1 + … a₁x + a₂x² + a₀

takový, aby součet čtverců odchylek mnohočlenu P_m (x) funkce f (x) v uzlových bodech

byl nejmenší. Funkce S (a₀, a₁, …, a_m) má extrém (minimum) tam, kde všechny

(k = 0, 1, …, m)

pro k = 0, 1, …, m; je to soustava normálních rovnic

Řešením této soustavy získáme hledané koeficienty. Této aproximace lze pak užít nejen v bodech {x_i}, ale také v jiných bodech x.

Pomocí maticového počtu lze dokázat, že problém nejmenších čtverců, a tedy i soustava , má jediné řešení.

Řešení normálních rovnic pro malé hodnoty m (m < 6) poskytuje velmi dobré aproximace. Avšak čím větší hodnoty m zvolíme, tím horší aproximace řešením normálních rovnic získáme. Volba stupně polynomu m (stupeň aproximujícího polynomu), je dána ve většině případů založena na znalosti fyzikální podstaty řešeného problému, tedy na znalosti teoretického očekávaného průběhu.

Numerický výpočet určitého integrálu.

Pokud nelze nalézt primitivní funkci, užíváme numerický výpočet určitého integrálu. Dále se budeme zabývat metodami s ekvidistantními uzly. Vzorce se dají odvodit jednoduše na základě geometrické interpretace určitého integrálu (plocha pod křivkou v daném intervalu). Ke stejným vztahům dospějeme použitím vzorců pro interpolaci.

Jedna se o výpočet určitého integrálu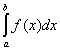, při kterém se užívá konečný počet hodnot funkce v intervalu <a,b> (tzv. kvadratura). V dalším výklad předpokládáme, že funkce je v uvedeném intervalu spojitá.

Obdélníkové pravidlo

Je nejjednodušším vzorcem pro kvadraturu a můžeme používat následující varianty:

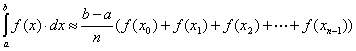nebo

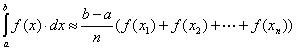Pro odhad chyby platí v obou případech vztah:

nebo složená obdélníková formule se středními uzlovými body

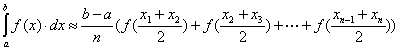Odhad chyby:

Obdélníkové pravidlo se v současné době k výpočtům téměř neužívá. Přesnější výsledky dává v převážné většině případů následující lichoběžníkové pravidlo.

Lichoběžníkové pravidlo

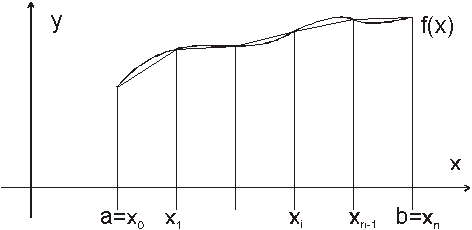
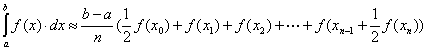
Odhad chyby:

Ze vzorce pro odhad chyby je možno stanovit přibližný počet dílků (segmentů) stejné délky, při zadané maximální povolené chybě.

Při znalosti průběhu druhé derivace integrované funkce a velikosti intervalu <a,b>, lze určit počet uzlů.

Má-li integrovaná funkce spojitou druhou derivaci, lze zvětšováním počtu úseků n zvětšovat přesnost výpočtu určitého integrálu.

Simpsonovo pravidlo

Daný interval rozdělíme na sudý počet podintervalů a v každém intervalu provádíme náhradu původní funkce parabolou (interpolačním polynomem druhého stupně).

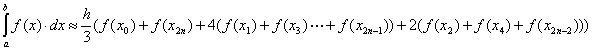
Odhad chyby:

Volba kvadraturního vzorce se neřídí nějakými pevnými pravidly. Obvykle ve většině případů vystačíme s užitím lichoběžníkového pravidla. Při větších nárocích na přesnost užijeme Simsonův vzorec. V některých případech, pokud známe hodnoty druhé, případně třetí derivace funkce v daných bodech, lze spočítat odhad chyby.

Příklad 1:

Určete hodnotu integrálu 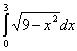(Řešení: ; grafem funkce f(x) je část kružnice o poloměru r=3 se středem v počátku souřadnicové soustavy).

Příklad 2: Určete integrál I= (Přesná hodnota je ln 3; I je přibližně 1,098 612)

Příklad 3: Určete integrál I= (I je přibližně 0,601 84)

Příklad 4: Určete integrál I= (Přesná hodnota je ln 2; I je přibližně0,693 15)

Příklad 5: Určete integrál I= 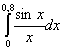(I je přibližně 0,772 096)

Simpsonovo pravidlo konverguje rychleji než lichoběžníkové pravidlo. Protože ve výrazech pro chyby vystupují vyšší derivace, je však lichoběžníkové pravidlo nejlepším vzorcem pro většinu problémů.

Rombergova metoda

Vychází z lichoběžníkové formule a dá se jednoduše implementovat na počítači. Protože ve většině případů vystačíme s dosud uváděnými metodami, nebudeme se touto metodou dále zabývat.

Řešení soustavy lineárních algebraických rovnic

Uvažujme soustavu n rovnic pro n neznámých ve tvaru:

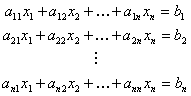maticový zápis: , koeficienty , jsou reálná čísla

Jinak: , i= 1, 2, …, n

a jsou vektory ; T značí transpozici. Matice A je řádu n. Při řešení soustavy rovnic s využitím Cramerova pravidla, kdy se neznámé určují pomocí determinantů, dochází ke značnému množství výpočtů. Např. při řešení 30 rovnic o 30 neznámých je nutno spočítat 31 determiantů řádu 30, což vede k 31*29*30! násobení tj. přibližně 2,3846232097116 . 10³⁵násobení. Pokud počítač provádí 10⁹ násobení za sekundu, řešení by bylo ukončeno za 7,5 . 10¹⁸ let. V mnoha případech je výhodné řešit soustavu s užitím inverzní matice. Aby výše uvedená soustava měla řešení, musí být matice koeficientů A typu nxn soustavy regulární. Determinant takové matice je nenulový. Dále předpokládáme, že řešíme nehomogenní soustavu, tedy, že vektor b je nenulový. Po násobení vektorem pravých stran získáváme řešení . Pro řešení lze využít např. tabulkový kalkulátor Excel. Při řešení soustavy rovnic se stovkami neznámých se mnohdy užívají numerické metody. Ty se v zásadě dělí na dvě skupiny. na metody přímé a metody iterační. V praxi se můžeme setkat jednak se soustavami s „plnými maticemi“, jednak se soustavami s „řídkými maticemi“ - ty mají málo nenulových prvků.

Špatně podmíněné soustavy

Soustava: 2 x+6 y = 8

2 x+6,00001 y = 8,00001

má řešení x = 1; y = 1

Soustava: 2 x+6 y = 8

2x+5,99999 y = 8,00002

má řešení x = 10; y = -2

Změna o 0,00002 u koeficientu a₂₂ a o 0,00001 v b₂ způsobila velkou změnu v řešení. Je to dáno tím, že determinant matice A se blíží k 0, koeficienty inverzní matice velké. Soustava se blíží ke stavu kdy nemá řešení. Úmyslně jsme použili označení x, y pro neznámé. Pak je možno rovnice převést na tvar y = k x + q, což jsou rovnice přímek. Souřadnice průsečíku obou přímek je řešením soustavy. Přímky jsou v našem případě „téměř shodné“.

Koeficienty druhé soustavy můžeme považovat za naměřené hodnoty koeficienty první soustavy. Velká chyba výsledku pak zcela znehodnocuje řešení.

Přímé metody (finitní)

U přímých metod získáme přesný výsledek, zanedbáme-li zaokrouhlovací chyby, při realizaci konečného počtu kroků. Principem přímých metod je eliminace neznámých. Nejstarší a nejznámější je Gausova eliminační metoda. Eliminace neznámých znamená jejich postupné vylučování. Elementárními operacemi s řádky získáme v přímém chodu z matice koeficientů A horní trojúhelníkovou matici (prvky pod hlavní diagonálou jsou nulové). Ve zpětném chodu (zpětná substituce) vypočítáváme vektor neznámých x. Můžeme využít ekvivalentních úprav: záměna pořadí rovnic, násobení obou stran rovnice jakýmkoli nenulovým reálným číslem, připočtení odpovídajících stran jakékoli rovnice k upravované rovnici. Pro algoritmické vyjádřená značíme

Při redukci matice soustavy A na trojúhelníkový tvar označíme . Předpokládáme, že matice je regulární a zároveň . Pokud tomu tak není, lze toho vždy dosáhnout přehozením rovnic. Prvek použitý k úpravě rovnic 2, ..., n nazýváme hlavním prvkem (pivot). Přičtením násobků 1. rovnice ke zbývajícím n-1 rovnicím vyloučíme (eliminujeme) neznámou z těchto rovnic. První rovnice se nemění. Přitom . Modifikovaná - první „redukovaná“ soustava (někdy se užívá název první přidružená soustava) soustava, má v 1. sloupci pod diagonálou samé 0:

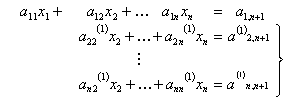soustava n-1 rovnic pro (n-1) neznámých, kde

V druhé fázi eliminace,za předpokladu, že , vyloučíme neznámou ze zbývajících n-2 rovnic redukované soustavy tak, že druhou rovnici redukované soustavy vynásobíme členy

a postupně přičteme tento násobek druhé rovnice ke zbývajícím (n – 3) rovnicím

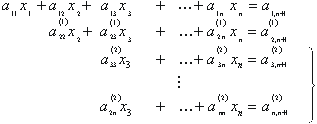soustava (n-2) rovnic o (n-2) neznámých kde

Pokračujeme pak analogickým způsobem, až po (n-1) krocích získáme výslednou redukovanou soustavu ve tvaru (horní index značí pořadí úpravy):

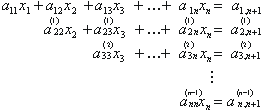
Tím je původní soustava převedena na trojúhelníkový tvar a k výpočtu řešení můžeme užít zpětné substituce.

, k=1,…,n-1; i=k+1,…,n; j=k+1,…,n+1

Provádíme postupně řádkové úpravy:

pro i £ k

, pro i > k

kde 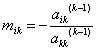(předpokl.: )

Normy matic

Přiřadíme-li čtvercové matici A číslo , které určíme podle následujících vztahů, získáme jistou míru velikosti matice.

Řádková norma (maximální řádkový součet)

Sloupcová norma (maximální sloupcový součet)

Eukleidovská norma

Při zkoumání konvergence u iteračních metod řešení soustav lineárních rovnic se normy užívají jako postačující podmínka konvergence: Jestliže řádková nebo sloupcová nebo euklidovská norma iterační matice H (viz dále) je menší než jedna, pak iterační metoda koverguje nezávisle na volbě počáteční aproximace .

Maticové iterační metody

Soustavu převedeme na ekvivalentní tvar vhodný pro iteraci: . Iterační metody dělíme na metody stacionární, které mají iterační matici H a vektor g konstantní a na metody nestacionární. Většina iteračních metod je stacionárních - matice H i vektor g se tedy po dobu výpočtu nemění. Pro analýzu i výpočet je to výhodné. U nestacionárních metod však lze urychlit konvergenci iteračních procesů.

Matice H je iterační matice. Pokud je splněno kriterium konvergence: jestliže je některá z norem matice H menší než jedna, pak metoda prosté iterace konverguje. Posloupnost iterací , pro k= 0, 1,… vede k řešení soustavy. Počáteční iterace (zahájení výpočtu) je v případě konvergentního procesu libovolná; často se užívá nulový vektor. Ukončení výpočtu provádíme mnohdy podmínkou , kde je jedna z vektorových norem a číslo d > 0. Jiný způsob je stanovení podmínky, kolik výpočtů máme provést. V současnosti se užívají různé iterační formule: Jacobiova, Gaussova-Saidlova, atd.

Postačující podmínkou konvergence je vztah Pak posloupnost uzrčená ze vztahu konverguje při libovolné volbě vektoru

Implementace numerických metod

V současné době je možno numerické metody implementovat s využitím různých programovacích jazyků a v různých prostředí. Běžné, a zcela vyhovující, je využití Visual Basicu (nebo Visual Basicu pro aplikace VBA - zde pozor na rychlost výpočtů; VBA užívá pouze interpret) a produktu Delphi. Zvláštní kategorií tvoří úlohy, které jsou implementovány v prostředí Internetu. Zde se využívá zejména Java nebo tzv. komponenty Active-X vytvářené v různých prostředích v kombinaci s dalšími metodami tvorby aktivních WWW stránek.

Při implementaci metod ve Visual Basicu (zejména ve Visual Basicu pro aplikace) je vhodné deklarovat proměnné. Jednak se vyhneme některým chybám při psaní programů, jednak připravíme podmínky pro urychlení procesů (výpočtů). Bez deklarace je používán univerzální typ Variant (22 bytů). Při výpočtech dochází ke zpomalení v aplikacích (např. v Excelu) neboť tam je užíván interpret (nedochází k vytváření exe souborů jako je tomu u Visual Basicu). Měřením časů výpočtů (např. s využitím funkce time) se o tom může každý přesvědčit.

Plzeň, prosinec 2000