Pokud se funkční hodnoty
f(
x
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaaiykaaaa@3A53@
funkce, zadané tabulkou:
|
x
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbaabeaaaaa@3804@
|
x
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIWaaabeaaaaa@37D0@
|
x
1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaaaaa@37D1@
|
x
2
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIYaaabeaaaaa@37D2@
|
…
|
x
n−1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaaaaa@39B1@
|
x
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGUbaabeaaaaa@3809@
|
(1)
|
|
y
i
=f(
x
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGPbaabeaakiabg2da9iaadAgacaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiaacMcaaaa@3D7B@
|
y
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIWaaabeaaaaa@37D1@
|
y
1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIXaaabeaaaaa@37D2@
|
y
2
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIYaaabeaaaaa@37D3@
|
…
|
y
n−1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaaaaa@39B2@
|
y
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbaabeaaaaa@380A@
|
shodují v
n+1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgUcaRiaaigdaaaa@389D@
bodech
[
x
i
,
y
i
]
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaaiilaiaaykW7caWG5bWaaSbaaSqaaiaadMgaaeqaaaGccaGLBbGaayzxaaaaaa@3E5E@
(uzlech interpolace) s hodnotou polynomu
P
n
(
x
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaabccacaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiaacMcaaaa@3C28@
,
tj.
|
f(
x
i
)=
P
n
(
x
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaaiykaiabg2da9iaadcfadaWgaaWcbaGaamOBaaqabaGccaqGGaGaaiikaiaadIhadaWgaaWcbaGaamyAaaqabaGccaGGPaaaaa@4193@
,
i=0, 1,…, n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaiabg2da9iaaicdacaGGSaGaaeiiaiaaigdacaGGSaGaeSOjGSKaaiilaiaabccacaWGUbaaaa@3EE1@
|
(2)
|
a tyto hodnoty považujeme za přesné, použijeme pro náhradu
funkce interpolační aproximaci nebo stručně interpolaci a sice nejčastěji interpolaci
polynomem n-tého stupně (polynomiální
interpolaci). Stupeň polynomu je tedy o jedna menší než je počet bodů v tabulce.
Tabulka (1)
může též reprezentovat reálnou funkci (viz následující obrázek) definovanou
v intervalu
〈a,b〉
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqeduuDJXwAKbYu51MyVXgaiuaacqWFPms4caWGHbGae8hlaWIaamOyaiab=PYiXdaa@4119@
.
Tedy funkce
y=f(x)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2da9iaadAgacaGGOaGaamiEaiaacMcaaaa@3B33@
je zadaná buď předpisem nebo tabulkou.
Tabulkové body mohou být buď ekvidistantní (mezi body jsou
stejné vzdálenosti) nebo na kroky tabulkových bodů neklademe žádné omezení. Ve
většině případů jsou tabulkové body ekvidistantní.
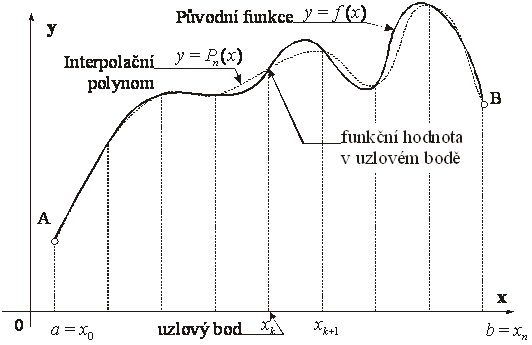
Obr. 1
Obr. 1 je geometrickou interpretací výše uvedeného popisu.
P
n
(x)=
a
n
x
n
+
a
n
x
n−1
+…
a
1
x +
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaabccacaGGOaGaamiEaiaacMcacqGH9aqpcaWGHbWaaSbaaSqaaiaad6gaaeqaaOGaamiEamaaCaaaleqabaGaamOBaaaakiabgUcaRiaadggadaWgaaWcbaGaamOBaaqabaGcdaWgaaWcbaGaeyOeI0IaaGymaaqabaGccaWG4bWaaWbaaSqabeaacaWGUbGaeyOeI0IaaGymaaaakiabgUcaRiablAciljaabccacaWGHbWaaSbaaSqaaiaaigdaaeqaaOGaamiEaiaabccacqGHRaWkcaqGGaGaaeiiaiaadggadaWgaaWcbaGaaGimaaqabaaaaa@52F0@
.
Hledáme takový polynom, aby platilo:
P
n
(
x
0
) = f(
x
0
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaabccacaGGOaGaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacaqGGaGaaeypaiaabccacaqGGaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaaaa@42CE@
,
P
n
(
x
1
) = f(
x
1
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaabccacaGGOaGaamiEamaaBaaaleaacaaIXaaabeaakiaacMcacaqGGaGaaeypaiaabccacaqGGaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaaaa@42D0@
,
…,
P
n
(
x
n
) = f(
x
n
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaabccacaGGOaGaamiEamaaBaaaleaacaWGUbaabeaakiaacMcacaqGGaGaaeypaiaabccacaqGGaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaaiykaaaa@4340@
.
Tedy v daných uzlových bodech souhlasí hodnoty aproximační funkce
s hodnotami aproximované funkce.
Získáme soustavu
n+1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgUcaRiaaigdaaaa@389D@
rovni o
n+1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgUcaRiaaigdaaaa@389D@
neznámých (jsou to koeficienty
a
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGPbaabeaaaaa@380D@
);
x
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbaabeaaaaa@3824@
a
f(
x
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeiiaiaadAgacaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiaacMcaaaa@3B15@
jsou známé hodnoty. Soustavu lze jednoduše
řešit, např. v aplikaci Excel, pomocí inverzní matice. Soustava je:
a
n
x
0
+
a
n
x
0
+
…
a
1
x
0
+
a
0
=
f(
x
0
)
a
n
x
1
+
a
n
x
1
+
…
a
1
x
1
+
a
0
=
f(
x
1
)
⋮
a
n
x
n
+
a
n
x
n
+
…
a
1
x
n
+
a
0
=
f(
x
n
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqbaeaabqGcaaaaaaqaaiaadggadaWgaaWcbaGaamOBaaqabaGccaWG4bWaaSbaaSqaaiaaicdaaeqaaOWaaWbaaSqabeaacaWGUbaaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaWGUbaabeaakmaaBaaaleaacqGHsislcaaIXaaabeaakiaadIhadaWgaaWcbaGaaGimaaqabaGcdaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaaGcbaGaey4kaScabaGaeSOjGSeabaGaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWcbaGaaGimaaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaaqaaiaadggadaWgaaWcbaGaamOBaaqabaGccaWG4bWaaSbaaSqaaiaaigdaaeqaaOWaaWbaaSqabeaacaWGUbaaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaWGUbaabeaakmaaBaaaleaacqGHsislcaaIXaaabeaakiaadIhadaWgaaWcbaGaaGymaaqabaGcdaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaaGcbaGaey4kaScabaGaeSOjGSeabaGaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWcbaGaaGymaaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaaqaaaqaaaqaaaqaaaqaaiabl6UinbqaaaqaaaqaaaqaaaqaaaqaaiaadggadaWgaaWcbaGaamOBaaqabaGccaWG4bWaaSbaaSqaaiaad6gaaeqaaOWaaWbaaSqabeaacaWGUbaaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaWGUbaabeaakmaaBaaaleaacqGHsislcaaIXaaabeaakiaadIhadaWgaaWcbaGaamOBaaqabaGcdaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaaGcbaGaey4kaScabaGaeSOjGSeabaGaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWcbaGaamOBaaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaaiykaaaaaaa@8E41@
Je-li interpolační funkce tvořena lineárními kombinacemi funkcí
sinkx, coskx
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4CaiaacMgacaGGUbGaam4AaiaadIhacaGGSaGaaGPaVlGacogacaGGVbGaai4CaiaadUgacaWG4baaaa@41AE@
,
kde
k=0,1,2,…
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2da9iaaicdacaGGSaGaaGymaiaacYcacaaIYaGaaiilaiablAcilbaa@3D47@
,
pak se jedná o interpolaci pomocí trigonometrických mnohočlenů či o
trigonometrickou interpolaci.
Po získání příslušných koeficientů interpolační funkce můžeme
zjistit snadno funkční hodnotu v jakémkoli bodě intervalu
〈a,b〉
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqeduuDJXwAKbYu51MyVXgaiuaacqWFPms4caWGHbGae8hlaWIaamOyaiab=PYiXdaa@4119@
.
Jiný způsob určení koeficientů interpolačního mnohočlenu je
užití Lagrangeova tvaru interpolačního mnohočlenu:
|
L
n
(x)=
(x−
x
1
)(x−
x
2
)…(x−
x
n
)
(
x
0
−
x
1
)(
x
0
−
x
2
)…(
x
0
−
x
n
)
y
0
+
(x−
x
0
)(x−
x
2
)…(x−
x
n
)
(
x
1
−
x
0
)(
x
1
−
x
2
)…(
x
1
−
x
n
)
y
1
+
…+
(x−
x
0
)(x−
x
1
)…(x−
x
i−1
)(x−
x
i+1
)…(x−
x
n
)
(
x
i
−
x
0
)(
x
i
−
x
1
)…(
x
i
−
x
i−1
)(
x
i
−
x
i+1
)…(
x
i
−
x
n
)
y
i
+
…+
(x−
x
0
)(x−
x
1
)…(x−
x
n−1
)
(
x
n
−
x
0
)(
x
n
−
x
1
)…(
x
n
−
x
n−1
)
y
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGmbWaaSbaaSqaaiaad6gaaeqaaOGaaiikaiaadIhacaGGPaGaeyypa0ZaaSaaaeaacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaaiykaiablAciljaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaakiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaaGimaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaaiykaiablAciljaacIcacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaakiaacMcaaaGaamyEamaaBaaaleaacaaIWaaabeaakiabgUcaRmaalaaabaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcacqWIMaYscaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGPaaabaGaaiikaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcacqWIMaYscaGGOaGaamiEamaaBaaaleaacaaIXaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGPaaaaiaadMhadaWgaaWcbaGaaGymaaqabaGccqGHRaWkaeaacqWIMaYscqGHRaWkdaWcaaqaaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaeSOjGSKaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaadMgacqGHsislcaaIXaaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaamyAaiabgUcaRiaaigdaaeqaaOGaaiykaiablAciljaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaakiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaamyAaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiablAciljaacIcacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGPbGaeyOeI0IaaGymaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaamyAaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaadMgacqGHRaWkcaaIXaaabeaakiaacMcacqWIMaYscaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaamOBaaqabaGccaGGPaaaaiaadMhadaWgaaWcbaGaamyAaaqabaGccqGHRaWkaeaacqWIMaYscqGHRaWkdaWcaaqaaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaeSOjGSKaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaWGUbaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaamOBaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiablAciljaacIcacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGPaaaaiaadMhadaWgaaWcbaGaamOBaaqabaaaaaa@025B@
|
(3)
|
Složitější úlohou interpolace, kterou se však nebudeme zabývat,
je to že kromě uváděných podmínek (2),
se ještě v některých uzlech předepisují derivace různých řádů interpolační
funkce.
Příklad 1.
Najděte interpolační mnohočlen pro funkci zadanou tabulkou:
|
i
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaaaa@36DC@
|
0
|
1
|
2
|
3
|
4
|
|
|
x
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbaabeaaaaa@3804@
|
0
|
1
|
2
|
3
|
4
|
(4)
|
|
yi = f(xi)
|
1
|
2
|
3
|
4
|
6
|
Řešení:
Hledaný mnohočlen bude čtvrtého stupně:
P
4
(x)=
a
4
x
4
+
a
3
x
3
+
a
2
x
2
+
a
1
x +
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaamiEaiaacMcacqGH9aqpcaWGHbWaaSbaaSqaaiaaisdaaeqaaOGaamiEamaaCaaaleqabaGaaGinaaaakiabgUcaRiaadggadaWgaaWcbaGaaG4maaqabaGccaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaamyyamaaBaaaleaacaaIYaaabeaakiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaqGGaGaamyyamaaBaaaleaacaaIXaaabeaakiaadIhacaqGGaGaey4kaSIaaeiiaiaabccacaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@51E7@
Z podmínek
P
4
(0)=1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaaGimaiaacMcacqGH9aqpcaaIXaaaaa@3C4D@
;
P
4
(1)=2
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaaGymaiaacMcacqGH9aqpcaaIYaaaaa@3C4F@
;
P
4
(2)=3
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaaGOmaiaacMcacqGH9aqpcaaIZaaaaa@3C51@
;
P
4
(3)=4
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaaG4maiaacMcacqGH9aqpcaaI0aaaaa@3C53@
;
P
4
(4)=6
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaaGinaiaacMcacqGH9aqpcaaI2aaaaa@3C56@
Získáme soustavu
0
4
a
4
+
0
3
a
3
+
0
2
a
2
+
0
a
1
+
a
0
=
1
1
4
a
4
+
1
3
a
3
+
1
2
a
2
+
1
a
1
+
a
0
=
2
2
4
a
4
+
2
3
a
3
+
2
2
a
2
+
2
a
1
+
a
0
=
3
3
4
a
4
+
3
3
a
3
+
3
2
a
2
+
3
a
1
+
a
0
=
4
4
4
a
4
+
4
3
a
3
+
4
2
a
2
+
4
a
1
+
a
0
=
6
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqbaeGabuWcaaaaaaqaaiaaicdadaahaaWcbeqaaiaaisdaaaGccaWGHbWaaSbaaSqaaiaaisdaaeqaaaGcbaGaey4kaScabaGaaGimamaaCaaaleqabaGaaG4maaaakiaadggadaWgaaWcbaGaaG4maaqabaaakeaacqGHRaWkaeaacaaIWaWaaWbaaSqabeaacaaIYaaaaOGaamyyamaaBaaaleaacaaIYaaabeaaaOqaaiabgUcaRaqaaiaaicdacaWGHbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaaIWaaabeaaaOqaaiabg2da9aqaaiaaigdaaeaacaaIXaWaaWbaaSqabeaacaaI0aaaaOGaamyyamaaBaaaleaacaaI0aaabeaaaOqaaiabgUcaRaqaaiaaigdadaahaaWcbeqaaiaaiodaaaGccaWGHbWaaSbaaSqaaiaaiodaaeqaaaGcbaGaey4kaScabaGaaGymamaaCaaaleqabaGaaGOmaaaakiaadggadaWgaaWcbaGaaGOmaaqabaaakeaacqGHRaWkaeaacaaIXaGaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiabgUcaRaqaaiaadggadaWgaaWcbaGaaGimaaqabaaakeaacqGH9aqpaeaacaaIYaaabaGaaGOmamaaCaaaleqabaGaaGinaaaakiaadggadaWgaaWcbaGaaGinaaqabaaakeaacqGHRaWkaeaacaaIYaWaaWbaaSqabeaacaaIZaaaaOGaamyyamaaBaaaleaacaaIZaaabeaaaOqaaiabgUcaRaqaaiaaikdadaahaaWcbeqaaiaaikdaaaGccaWGHbWaaSbaaSqaaiaaikdaaeqaaaGcbaGaey4kaScabaGaaGOmaiaadggadaWgaaWcbaGaaGymaaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaaG4maaqaaiaaiodadaahaaWcbeqaaiaaisdaaaGccaWGHbWaaSbaaSqaaiaaisdaaeqaaaGcbaGaey4kaScabaGaaG4mamaaCaaaleqabaGaaG4maaaakiaadggadaWgaaWcbaGaaG4maaqabaaakeaacqGHRaWkaeaacaaIZaWaaWbaaSqabeaacaaIYaaaaOGaamyyamaaBaaaleaacaaIYaaabeaaaOqaaiabgUcaRaqaaiaaiodacaWGHbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaaIWaaabeaaaOqaaiabg2da9aqaaiaaisdaaeaacaaI0aWaaWbaaSqabeaacaaI0aaaaOGaamyyamaaBaaaleaacaaI0aaabeaaaOqaaiabgUcaRaqaaiaaisdadaahaaWcbeqaaiaaiodaaaGccaWGHbWaaSbaaSqaaiaaiodaaeqaaaGcbaGaey4kaScabaGaaGinamaaCaaaleqabaGaaGOmaaaakiaadggadaWgaaWcbaGaaGOmaaqabaaakeaacqGHRaWkaeaacaaI0aGaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiabgUcaRaqaaiaadggadaWgaaWcbaGaaGimaaqabaaakeaacqGH9aqpaeaacaaI2aaaaaaa@9BC9@
tedy
a
0
=
1
a
4
+
a
3
+
a
2
+
a
1
+
a
0
=
2
16
a
4
+
8
a
3
+
4
a
2
+
2
a
1
+
a
0
=
3
81
a
4
+
27
a
3
+
9
a
2
+
3
a
1
+
a
0
=
4
256
a
4
+
64
a
3
+
16
a
2
+
4
a
1
+
a
0
=
6
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqbaeGabuWcaaaaaaqaaaqaaaqaaaqaaaqaaaqaaaqaaaqaaaqaaiaadggadaWgaaWcbaGaaGimaaqabaaakeaacqGH9aqpaeaacaaIXaaabaGaamyyamaaBaaaleaacaaI0aaabeaaaOqaaiabgUcaRaqaaiaadggadaWgaaWcbaGaaG4maaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaikdaaeqaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiabgUcaRaqaaiaadggadaWgaaWcbaGaaGimaaqabaaakeaacqGH9aqpaeaacaaIYaaabaGaaGymaiaaiAdacaWGHbWaaSbaaSqaaiaaisdaaeqaaaGcbaGaey4kaScabaGaaGioaiaadggadaWgaaWcbaGaaG4maaqabaaakeaacqGHRaWkaeaacaaI0aGaamyyamaaBaaaleaacaaIYaaabeaaaOqaaiabgUcaRaqaaiaaikdacaWGHbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaaIWaaabeaaaOqaaiabg2da9aqaaiaaiodaaeaacaaI4aGaaGymaiaadggadaWgaaWcbaGaaGinaaqabaaakeaacqGHRaWkaeaacaaIYaGaaG4naiaadggadaWgaaWcbaGaaG4maaqabaaakeaacqGHRaWkaeaacaaI5aGaamyyamaaBaaaleaacaaIYaaabeaaaOqaaiabgUcaRaqaaiaaiodacaWGHbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaey4kaScabaGaamyyamaaBaaaleaacaaIWaaabeaaaOqaaiabg2da9aqaaiaaisdaaeaacaaIYaGaaGynaiaaiAdacaWGHbWaaSbaaSqaaiaaisdaaeqaaaGcbaGaey4kaScabaGaaGOnaiaaisdacaWGHbWaaSbaaSqaaiaaiodaaeqaaaGcbaGaey4kaScabaGaaGymaiaaiAdacaWGHbWaaSbaaSqaaiaaikdaaeqaaaGcbaGaey4kaScabaGaaGinaiaadggadaWgaaWcbaGaaGymaaqabaaakeaacqGHRaWkaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaaGOnaaaaaaa@8206@
Soustavu lze zapsat v maticovém tvaru
Aa=b
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqaiaahggacqGH9aqpcaWHIbaaaa@3992@
kde
A=[
0
0
0
0
1
1
1
1
1
1
16
8
4
2
1
81
27
9
3
1
256
64
16
4
1
]
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqaiabg2da9maadmaabaqbaeGGbuqbaaaaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaGymaaqaaiaaigdaaeaacaaIXaaabaGaaGymaiaaiAdaaeaacaaI4aaabaGaaGinaaqaaiaaikdaaeaacaaIXaaabaGaaGioaiaaigdaaeaacaaIYaGaaG4naaqaaiaaiMdaaeaacaaIZaaabaGaaGymaaqaaiaaikdacaaI1aGaaGOnaaqaaiaaiAdacaaI0aaabaGaaGymaiaaiAdaaeaacaaI0aaabaGaaGymaaaaaiaawUfacaGLDbaaaaa@51F9@
b=[
1
2
3
4
6
]
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCOyaiabg2da9maadmaabaqbaeGabuqaaaaabaGaaGymaaqaaiaaikdaaeaacaaIZaaabaGaaGinaaqaaiaaiAdaaaaacaGLBbGaayzxaaaaaa@3D96@
Pak
a=
A
-1
b
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyyaiabg2da9iaahgeadaahaaWcbeqaaiaah2cacaWHXaaaaOGaaCOyaaaa@3B39@
,
kde
A
-1
=[
0,04167
−0,16667
0,25
−0,16667
0,04167
−0,41667
1,5
−2
1,16667
−0,25
1,45833
−4,33333
4,75
−2,33333
0,45833
−2,08333
4
−3
1,33333
−0,25
1
0
0
0
0
]
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqamaaCaaaleqabaGaaCylaiaahgdaaaGccqGH9aqpdaWadaqaauaabqyafuaaaaaabaGaaGimaiaacYcacaaIWaGaaGinaiaaigdacaaI2aGaaG4naaqaaiabgkHiTiaaicdacaGGSaGaaGymaiaaiAdacaaI2aGaaGOnaiaaiEdaaeaacaaIWaGaaiilaiaaikdacaaI1aaabaGaeyOeI0IaaGimaiaacYcacaaIXaGaaGOnaiaaiAdacaaI2aGaaG4naaqaaiaaicdacaGGSaGaaGimaiaaisdacaaIXaGaaGOnaiaaiEdaaeaacqGHsislcaaIWaGaaiilaiaaisdacaaIXaGaaGOnaiaaiAdacaaI3aaabaGaaGymaiaacYcacaaI1aaabaGaeyOeI0IaaGOmaaqaaiaaigdacaGGSaGaaGymaiaaiAdacaaI2aGaaGOnaiaaiEdaaeaacqGHsislcaaIWaGaaiilaiaaikdacaaI1aaabaGaaGymaiaacYcacaaI0aGaaGynaiaaiIdacaaIZaGaaG4maaqaaiabgkHiTiaaisdacaGGSaGaaG4maiaaiodacaaIZaGaaG4maiaaiodaaeaacaaI0aGaaiilaiaaiEdacaaI1aaabaGaeyOeI0IaaGOmaiaacYcacaaIZaGaaG4maiaaiodacaaIZaGaaG4maaqaaiaaicdacaGGSaGaaGinaiaaiwdacaaI4aGaaG4maiaaiodaaeaacqGHsislcaaIYaGaaiilaiaaicdacaaI4aGaaG4maiaaiodacaaIZaaabaGaaGinaaqaaiabgkHiTiaaiodaaeaacaaIXaGaaiilaiaaiodacaaIZaGaaG4maiaaiodacaaIZaaabaGaeyOeI0IaaGimaiaacYcacaaIYaGaaGynaaqaaiaaigdaaeaacaaIWaaabaGaaGimaaqaaiaaicdaaeaacaaIWaaaaaGaay5waiaaw2faaaaa@9678@
a=[
0,04167
−0,25
0,45833
0,75
1
]
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyyaiabg2da9maadmaabaqbaeaHbuqaaaaabaGaaGimaiaacYcacaaIWaGaaGinaiaaigdacaaI2aGaaG4naaqaaiabgkHiTiaaicdacaGGSaGaaGOmaiaaiwdaaeaacaaIWaGaaiilaiaaisdacaaI1aGaaGioaiaaiodacaaIZaaabaGaaGimaiaacYcacaaI3aGaaGynaaqaaiaaigdaaaaacaGLBbGaayzxaaaaaa@4C1D@
tedy
a
4
=
0,04167
a
3
=
−0,25
a
2
=
0,45833
a
1
=
0,75
a
0
=
1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqbaeabbuWaaaaabaGaamyyamaaBaaaleaacaaI0aaabeaaaOqaaiabg2da9aqaaiaaicdacaGGSaGaaGimaiaaisdacaaIXaGaaGOnaiaaiEdaaeaacaWGHbWaaSbaaSqaaiaaiodaaeqaaaGcbaGaeyypa0dabaGaeyOeI0IaaGimaiaacYcacaaIYaGaaGynaaqaaiaadggadaWgaaWcbaGaaGOmaaqabaaakeaacqGH9aqpaeaacaaIWaGaaiilaiaaisdacaaI1aGaaGioaiaaiodacaaIZaaabaGaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiabg2da9aqaaiaaicdacaGGSaGaaG4naiaaiwdaaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaeyypa0dabaGaaGymaaaaaaa@561D@
Hledaný mnohočlen je
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcaa@35ED@
P
4
(x)=0,04167
x
4
+−0,25
x
3
+0,45833
x
2
+ 0,75x + 1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaI0aaabeaakiaabccacaGGOaGaamiEaiaacMcacqGH9aqpcaaIWaGaaiilaiaaicdacaaI0aGaaGymaiaaiAdacaaI3aGaamiEamaaCaaaleqabaGaaGinaaaakiabgUcaRiabgkHiTiaaicdacaGGSaGaaGOmaiaaiwdacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaaGimaiaacYcacaaI0aGaaGynaiaaiIdacaaIZaGaaG4maiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaqGGaGaaGimaiaacYcacaaI3aGaaGynaiaadIhacaqGGaGaey4kaSIaaeiiaiaabccacaaIXaaaaa@5A71@
Příklad 2.
Funkce je dána tabulkou
|
i
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaaaa@36DC@
|
0
|
1
|
2
|
3
|
|
|
x
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbaabeaaaaa@3804@
|
-2
|
-1
|
0
|
2
|
(5)
|
|
yi = f(xi)
|
5
|
-4
|
-5
|
-7
|
Určete interpolační mnohočlen ve tvaru (3).
L
n
(x)=
(x−
x
1
)(x−
x
2
)(x−
x
3
)
(
x
0
−
x
1
)(
x
0
−
x
2
)(
x
0
−
x
3
)
y
0
+
(x−
x
0
)(x−
x
2
)(x−
x
3
)
(
x
1
−
x
0
)(
x
1
−
x
2
)(
x
1
−
x
3
)
y
1
+
(x−
x
0
)(x−
x
1
)(x−
x
3
)
(
x
2
−
x
0
)(
x
2
−
x
1
)(
x
2
−
x
3
)
y
2
+
(x−
x
0
)(x−
x
1
)(x−
x
2
)
(
x
3
−
x
0
)(
x
3
−
x
1
)(
x
3
−
x
2
)
y
3
=
(x+1)x(x−2)
(−2+1)(−2)(−2−2)
5+
(x+2)x(x−2)
(−1+2)(−1)(−1−2)
(−4)+
(x+2)(x+1)(x−2)
(+2)(−1)(2)
(−5)+
(x+2)(x+1)x
(2+2)(2+1)(2)
(−7)=
(x+1)x(x−2)
−8
5+
(x+2)x(x−2)
3
(−4)+
(x+2)(x+1)(x−2)
−4
(−5)+
(x+2)(x+1)x
24
(−7)=
-
x
3
+
x
2
+x-5
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaWabeaacaWGmbWaaSbaaSqaaiaad6gaaeqaaOGaaiikaiaadIhacaGGPaGaeyypa0ZaaSaaaeaacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaaiykaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIZaaabeaakiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaaGimaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaaiykaiaacIcacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIZaaabeaakiaacMcaaaGaamyEamaaBaaaleaacaaIWaaabeaakiabgUcaRmaalaaabaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaG4maaqabaGccaGGPaaabaGaaiikaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcacaGGOaGaamiEamaaBaaaleaacaaIXaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaG4maaqabaGccaGGPaaaaiaadMhadaWgaaWcbaGaaGymaaqabaGccqGHRaWkaeaadaWcaaqaaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaiodaaeqaaOGaaiykaaqaaiaacIcacaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacaGGOaGaamiEamaaBaaaleaacaaIYaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaaGOmaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaiodaaeqaaOGaaiykaaaacaWG5bWaaSbaaSqaaiaaikdaaeqaaOGaey4kaSYaaSaaaeaacaGGOaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaGccaGGPaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiaacIcacaWG4bGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaaIZaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaGccaGGPaGaaiikaiaadIhadaWgaaWcbaGaaG4maaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiaacIcacaWG4bWaaSbaaSqaaiaaiodaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIYaaabeaakiaacMcaaaGaamyEamaaBaaaleaacaaIZaaabeaakiabg2da9aqaamaalaaabaGaaiikaiaadIhacqGHRaWkcaaIXaGaaiykaiaadIhacaGGOaGaamiEaiabgkHiTiaaikdacaGGPaaabaGaaiikaiabgkHiTiaaikdacqGHRaWkcaaIXaGaaiykaiaacIcacqGHsislcaaIYaGaaiykaiaacIcacqGHsislcaaIYaGaeyOeI0IaaGOmaiaacMcaaaGaaGynaiabgUcaRmaalaaabaGaaiikaiaadIhacqGHRaWkcaaIYaGaaiykaiaadIhacaGGOaGaamiEaiabgkHiTiaaikdacaGGPaaabaGaaiikaiabgkHiTiaaigdacqGHRaWkcaaIYaGaaiykaiaacIcacqGHsislcaaIXaGaaiykaiaacIcacqGHsislcaaIXaGaeyOeI0IaaGOmaiaacMcaaaGaaiikaiabgkHiTiaaisdacaGGPaGaey4kaScabaWaaSaaaeaacaGGOaGaamiEaiabgUcaRiaaikdacaGGPaGaaiikaiaadIhacqGHRaWkcaaIXaGaaiykaiaacIcacaWG4bGaeyOeI0IaaGOmaiaacMcaaeaacaGGOaGaey4kaSIaaGOmaiaacMcacaGGOaGaeyOeI0IaaGymaiaacMcacaGGOaGaaGOmaiaacMcaaaGaaiikaiabgkHiTiaaiwdacaGGPaGaey4kaSYaaSaaaeaacaGGOaGaamiEaiabgUcaRiaaikdacaGGPaGaaiikaiaadIhacqGHRaWkcaaIXaGaaiykaiaadIhaaeaacaGGOaGaaGOmaiabgUcaRiaaikdacaGGPaGaaiikaiaaikdacqGHRaWkcaaIXaGaaiykaiaacIcacaaIYaGaaiykaaaacaGGOaGaeyOeI0IaaG4naiaacMcacqGH9aqpaeaadaWcaaqaaiaacIcacaWG4bGaey4kaSIaaGymaiaacMcacaWG4bGaaiikaiaadIhacqGHsislcaaIYaGaaiykaaqaaiabgkHiTiaaiIdaaaGaaGynaiabgUcaRmaalaaabaGaaiikaiaadIhacqGHRaWkcaaIYaGaaiykaiaadIhacaGGOaGaamiEaiabgkHiTiaaikdacaGGPaaabaGaaG4maaaacaGGOaGaeyOeI0IaaGinaiaacMcacqGHRaWkaeaadaWcaaqaaiaacIcacaWG4bGaey4kaSIaaGOmaiaacMcacaGGOaGaamiEaiabgUcaRiaaigdacaGGPaGaaiikaiaadIhacqGHsislcaaIYaGaaiykaaqaaiabgkHiTiaaisdaaaGaaiikaiabgkHiTiaaiwdacaGGPaGaey4kaSYaaSaaaeaacaGGOaGaamiEaiabgUcaRiaaikdacaGGPaGaaiikaiaadIhacqGHRaWkcaaIXaGaaiykaiaadIhaaeaacaaIYaGaaGinaaaacaGGOaGaeyOeI0IaaG4naiaacMcacqGH9aqpaeaacaGGTaGaamiEamaaCaaaleqabaGaaG4maaaakiabgUcaRiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWG4bGaaiylaiaaiwdaaaaa@704A@
Výsledný polynom je tedy
P
3
(x)=-
x
3
+
x
2
+x-5
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaIZaaabeaakiaacIcacaWG4bGaaiykaiabg2da9iaac2cacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacaGGTaGaaGynaaaa@43F4@
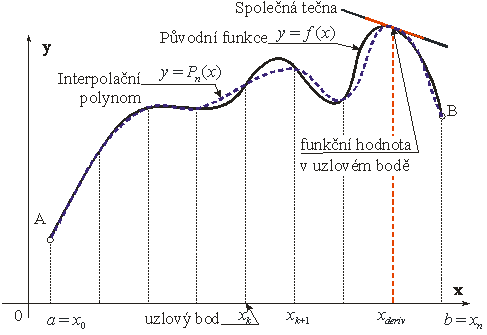
Obr. 2
Všimněte si shodné první derivace v uzlovém bodě
x
deriv
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGKbGaamyzaiaadkhacaWGPbGaamODaaqabaaaaa@3BCA@
na Obr.
2
Význam interpolace v současné době spočívá zejména
v tom, že je východiskem pro některé další numerické metody jako například
metody numerického integrování funkcí (ty budou v rámci tohoto modulu
uvedeny) aj.
Polynomiální interpolace je stupně
n
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaaaa@36E1@
,
když interpolační mnohočlen je stupně
n
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaaaa@36E1@
.
Interpolace je lineární, tehdy, je-li interpolační mnohočlen stupně 1 nebo 0.
Polynomiální interpolace je kvadratická resp. kubická, když je interpolační
mnohočlen stupně 2 resp. 3.
Příklad 3.
Jaký je tvar Lagrangeova mnohočlenu, pro lineární interpolaci,
jsou li dány hodnoty
(
x
i
,
y
i
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamyAaaqabaGccaGGSaGaamyEamaaBaaaleaacaWGPbaabeaakiaacMcaaaa@3C3A@
,
i=0,1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaiabg2da9iaaicdacaGGSaGaaGymaaaa@3A07@
Odpověď:
L
n
(x)=
(x−
x
1
)
(
x
0
−
x
1
)
y
0
+
(x−
x
0
)
(
x
1
−
x
0
)
y
1
=
y
0
+
y
1
−
y
0
x
1
−
x
0
(x−
x
0
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamitamaaBaaaleaacaWGUbaabeaakiaacIcacaWG4bGaaiykaiabg2da9maalaaabaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaaqaaiaacIcacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIXaaabeaakiaacMcaaaGaamyEamaaBaaaleaacaaIWaaabeaakiabgUcaRmaalaaabaGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaaqaaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIWaaabeaakiaacMcaaaGaamyEamaaBaaaleaacaaIXaaabeaakiabg2da9iaadMhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkdaWcaaqaaiaadMhadaWgaaWcbaGaaGymaaqabaGccqGHsislcaWG5bWaaSbaaSqaaiaaicdaaeqaaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaaaaOGaaiikaiaadIhacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaaiykaaaa@698D@
Grafem funkce v kartézské soustavě souřadnic je přímka se
směrnicí
y
1
−
y
0
x
1
−
x
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWG5bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaamyEamaaBaaaleaacaaIWaaabeaaaOqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaaaaaaa@3FA5@

