Metoda Monte Carlo výpočtu určitého integrálu

Existuje více typů metod Monte Carlo. Tyto metody vychází z teorie pravděpodobnosti. Umožňující výpočet parametrů modelu nikoli přímým řešením, ale napodobením (simulací) chodu modelu. Mnohonásobná simulace umožní výpočet parametrů jednoduchými statistickými metodami.

Např. střední hodnota spojité náhodné veličiny se složitou hustotou pravděpodobnosti se namísto výpočtu složitého integrálu určí metodou Monte Carlo tak, že se pomocí náhodných čísel vypočte velké množství hodnot této náhodné veličiny a její střední hodnota se stanoví s libovolnou přesností jako aritmetický průměr vypočtených hodnot (náhodná čísla).

S využitím věty o střední hodnotě můžeme u integrace metodou Monte Carlo u jednorozměrných integrálů tedy použít vztah

I(f)= ∫ a b f(x)dx ≈ (b−a) n ∑ i=1 n f( x i ) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiaacIcacaWGMbGaaiykaiabg2da9maapehabaGaamOzaiaacIcacaWG4bGaaiykaiaadsgacaWG4baaleaacaWGHbaabaGaamOyaaqdcqGHRiI8aOGaeyisIS7aaSaaaeaacaGGOaGaamOyaiabgkHiTiaadggacaGGPaaabaGaamOBaaaadaaeWbqaaiaadAgacaGGOaGaamiEamaaBaaaleaacaWGPbaabeaakiaacMcaaSqaaiaadMgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aaaa@549C@

kde { x i } MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaacaWG4bWaaSbaaSqaaiaadMgaaeqaaaGccaGL7bGaayzFaaaaaa@3A5F@  je množina náhodně generovaných bodů (hodnot nezávisle proměnné). Při výpočtu se užívá generátor pseudonáhodných čísel na jehož kvalitě extrémně záleží.

Příklad 1.

∫ 0 3 9− x 2 dx≈ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaadaGcaaqaaiaaiMdacqGHsislcaWG4bWaaWbaaSqabeaacaaIYaaaaaqabaaabaGaaGimaaqaaiaaiodaa0Gaey4kIipakiaadsgacaWG4bGaeyisISlaaa@4129@  7,06858

Příklad algoritmu (rozptyl výsledků je poměrně velký vhledem k nedokonalému generátoru náhodných čísel!):

function TForm1.F(X:extended): extended;

begin

F:=sqrt(9-sqr(x));

end;

procedure TForm1.Button2Click(Sender: TObject);

var x,Integral,Suma:extended;

    n,k:Integer ;

begin

  Randomize;

  n:=StrToInt(edit3.text);

  Suma:=0;

  for k:=1 to n do

  begin

  x:=Random*3;

  Suma:=Suma+F(x);

  end;

  Integral:=(3*Suma) /n;

  edit4.text:=FloatToStr(Integral);

  Button2.Caption:='Spočteno';

end;

Jiný algoritmus je založen na opakovaném provádění testu (který je označen buď jako úspěšný, pak vrací hodnotu true nebo neúspěšný, pak vrací hodnotu false)

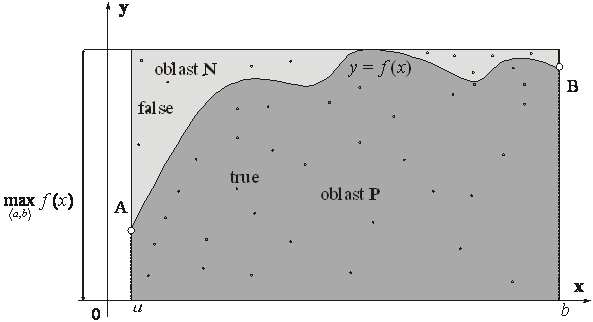
U jednorozměrných integrálů můžeme též volit opakovaně dvojici náhodných čísel [ x i , y i ] MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaaiilaiaadMhadaWgaaWcbaGaamyAaaqabaaakiaawUfacaGLDbaaaaa@3CF2@ . Přitom x i ∈〈a,b〉; y i ∈〈0, max⁡ 〈a,b〉 f(x)〉 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbaabeaakiabgIGiolabgMYiHlaadggacaGGSaGaamOyaiabgQYiXlaacUdacaWG5bWaaSbaaSqaaiaadMgaaeqaaOGaeyicI4SaeyykJeUaaGimaiaacYcadaWfqaqaaiGac2gacaGGHbGaaiiEaaWcbaGaeyykJeUaamyyaiaacYcacaWGIbGaeyOkJepabeaakiaadAgacaGGOaGaamiEaiaacMcacqGHQms8aaa@555C@

Pak podíl úspěšných testů ( f( x i )≥ y i MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaadMgaaeqaaOGaaiykaiabgwMiZkaadMhadaWgaaWcbaGaamyAaaqabaaaaa@3E50@  ) a celkového množství testů n MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaaaa@3700@  (pro velký počet testů) násobený plochou obdélníka jehož jedna strana je b−a MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyaiabgkHiTiaadggaaaa@38C7@  a druhá max⁡ 〈a,b〉 f(x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGTbGaaiyyaiaacIhaaSqaaiabgMYiHlaadggacaGGSaGaamOyaiabgQYiXdqabaGccaWGMbGaaiikaiaadIhacaGGPaaaaa@4265@ , tedy P=(b−a) max⁡ 〈a,b〉 f(x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2da9iaacIcacaWGIbGaeyOeI0IaamyyaiaacMcadaWfqaqaaiGac2gacaGGHbGaaiiEaaWcbaGaeyykJeUaamyyaiaacYcacaWGIbGaeyOkJepabeaakiaadAgacaGGOaGaamiEaiaacMcaaaa@4853@ , je přibližnou hodnotou integrálu dané funkce na daném intervalu.

Při výpočtu integrálu metodou Monte Carlo uvedeným druhým způsobem určíme hraniční funkční hodnotu. Opět je nutno připomenout, že nevhodným generováním pseudonáhodných čísel mohou vznikat chyby při výpočtu (větší rozptyl výsledků).

Příklad 2.

∫ 0 3 9− x 2 dx≈ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaadaGcaaqaaiaaiMdacqGHsislcaWG4bWaaWbaaSqabeaacaaIYaaaaaqabaaabaGaaGimaaqaaiaaiodaa0Gaey4kIipakiaadsgacaWG4bGaeyisISlaaa@4129@  7,06858

Příklad algoritmu pro experimentování (funkce je táž jako v předchozím příkladu):

procedure TForm1.Button1Click(Sender: TObject);

var x,y,Integral:extended;

    n,k,Uspech:Integer ;

begin

  Randomize;

  n:=StrToInt(edit3.text);

  Uspech:=0;

  for k:=1 to n do

  begin

  x:=Random*3;

  y:=Random*3;

  if (F(x)>=y) then

  Inc(Uspech);

  end;

  Integral:=(9*Uspech) /n;

  edit4.text:=FloatToStr(Integral);

  Button1.Caption:='Spočteno';

end;

 

 

Uvádí se, že metoda Monte Carlo°je vhodná pro výpočet vícerozměrných (dvojných, trojných) integrálů.

V aplikaci Mathematica je k dispozici příkaz NIntegrate:

Příklad:

NIntegrate[If[x^2+y^2+z^2<1,1,0],{x,-1,1},{y,-1,1},{z,-1,1},MaxPoints®10000]

výsledek je:

4,18106

Přesná hodnota v příkladu uváděného integrálu je 4 3 π MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaaI0aaabaGaaG4maaaacqaHapaCaaa@3936@  (pro stejný počet míst: 4,18879)